เซต ม.4 เป็นบทเรียนแรกที่นักเรียน ม.ปลาย จะได้เจอในวิชาคณิตศาสตร์ และถือเป็นรากฐานสำคัญที่จะต้องเข้าใจให้แม่นยำ เพราะความรู้เรื่องเซตจะถูกนำไปใช้ในเกือบทุกบทของคณิตศาสตร์ระดับมัธยมปลาย วันนี้เราจะมาทำความเข้าใจเรื่องเซตกันแบบง่ายๆ ที่ใครก็เข้าใจได้!
✨ทำไมต้องเรียนเรื่องเซต?
เซต ไม่ใช่แค่เรื่องยากๆ ที่ต้องท่องจำ แต่เป็นเครื่องมือที่จะช่วยให้เราเข้าใจคณิตศาสตร์ขั้นสูงได้ดีขึ้น เรื่องเซตจะถูกนำไปใช้ในหัวข้อต่างๆ เช่น:
- – ความสัมพันธ์และฟังก์ชัน – ใช้เซตในการกำหนดโดเมนและเรนจ์
- – จำนวนจริง – จัดประเภทจำนวนด้วยแนวคิดเซต
- – แคลคูลัส – ใช้เซตในการกำหนดขอบเขตและช่วง
- – ความน่าจะเป็น – sample space คือเซตของผลลัพธ์ที่เป็นไปได้ทั้งหมด
หลักการง่ายๆ คือ ถ้าเซตแข็งแกร่ง คณิตศาสตร์ทั้งหมดก็แข็งแกร่งตาม!
✨ เซตคืออะไร? เข้าใจได้ใน 1 นาที
เซต คือการรวบรวมสิ่งต่างๆ ที่มีลักษณะเฉพาะเหมือนกัน เหมือนการจัดของในกล่องต่างๆ ตามประเภท
ตัวอย่างในชีวิตจริง:
- – เซตของนักเรียนในห้อง ม.4/1 = {สมชาย, สมหญิง, สมศักดิ์, …}
- – เซตของผลไม้ = {แอปเปิ้ล, ส้ม, กล้วย, มะม่วง}
- – เซตของเลขคู่ที่น้อยกว่า 10 = {2, 4, 6, 8}
✨2 วิธีเขียนเซตที่ต้องเข้าใจ
1. แบบแจกแจงสมาชิก (Roster Method)
เขียนสมาชิกทุกตัวในเครื่องหมาย { } และคั่นด้วยเครื่องหมายจุลภาค
ตัวอย่าง: A = {1, 2, 3, 4, 5}
2. แบบบอกเงื่อนไข (Set-builder Notation)
ใช้เมื่อสมาชิกมีจำนวนมากหรือไม่สามารถเขียนหมดได้
สัญลักษณ์ที่ต้องรู้:
- – ℕ = จำนวนนับ (1, 2, 3, …)
- – ℤ = จำนวนเต็ม (…, -2, -1, 0, 1, 2, …)
- – ℝ = จำนวนจริง
- – ∈ = เป็นสมาชิกของ
- – | = “โดยที่” หรือ “ซึ่ง”
ตัวอย่าง: A = {x ∈ ℕ | x < 6} หมายถึง A = {1, 2, 3, 4, 5}
✨ประเภทของเซตที่ต้องจำ
1. เซตจำกัด (Finite Set)
นับจำนวนสมาชิกได้หมด เช่น เซตของวันในสัปดาห์ = {จันทร์, อังคาร, …, อาทิตย์}
2. เซตอนันต์ (Infinite Set)
มีสมาชิกไม่สิ้นสุด เช่น เซตของจำนวนนับ = {1, 2, 3, 4, …}
3. เซตว่าง (Empty Set)
ไม่มีสมาชิกเลย เขียนแทนด้วย ∅ หรือ { }
✨สับเซต: เข้าใจผ่านการเปรียบเทียบ
สับเซต เหมือนกับการที่กล่องเล็กอยู่ในกล่องใหญ่
A เป็นสับเซตของ B (เขียน A ⊆ B) หมายความว่า สมาชิกทุกตัวของ A เป็นสมาชิกของ B ด้วย
ตัวอย่างง่ายๆ:
- – เซตของนักเรียนชาย ⊆ เซตของนักเรียนทั้งหมด
- – {1, 3} ⊆ {1, 2, 3, 4, 5}
เทคนิคจำ: จำนวนสับเซตทั้งหมดของเซตที่มี n สมาชิก = 2ⁿ
✨เพาเวอร์เซต: แนวคิดที่เท่มาก
เพาเวอร์เซต P(A) คือเซตที่ประกอบด้วยสับเซตทั้งหมดของ A
ตัวอย่าง: ถ้า A = {1, 2}
- – สับเซตของ A คือ: ∅, {1}, {2}, {1, 2}
- – ดังนั้น P(A) = {∅, {1}, {2}, {1, 2}}
✨แผนภาพเวนน์: เห็นภาพชัดขึ้น
แผนภาพเวนน์ คือการวาดเซตเป็นวงกลมเพื่อให้เห็นภาพความสัมพันธ์ระหว่างเซต วิธีนี้จะช่วยให้เข้าใจการดำเนินการของเซตได้ง่ายมาก!
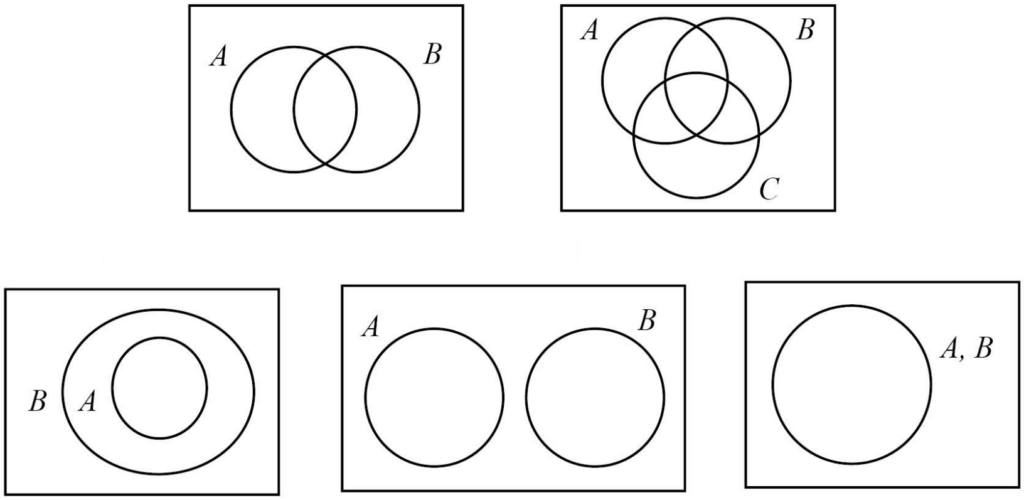
✨4 การดำเนินการของเซตที่ต้องเชี่ยวชาญ
1. ยูเนียน (Union) A ∪ B
ความหมาย: สมาชิกที่อยู่ใน A หรือ B หรือทั้งคู่ จำง่ายๆ: รวมทุกอย่างเข้าด้วยกัน แต่ไม่ซ้ำ
2. อินเตอร์เซคชัน (Intersection) A ∩ B
ความหมาย: สมาชิกที่อยู่ใน A และ B พร้อมกัน จำง่ายๆ: เอาเฉพาะส่วนที่ซ้ำกัน
3. ผลต่าง (Difference) A – B
ความหมาย: สมาชิกที่อยู่ใน A แต่ไม่อยู่ใน B
จำง่ายๆ: เอา A แล้วตัดส่วนที่ซ้ำกับ B ออก
4. คอมพลีเมนต์ (Complement) A’
ความหมาย: สมาชิกที่อยู่ในเอกภพ U แต่ไม่อยู่ใน A จำง่ายๆ: ทุกอย่างที่ไม่ใช่ A
✨สูตรมหาเทพที่ช่วยแก้โจทย์
สำหรับ 2 เซต:
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
สูตรนี้เป็นเหมือนกุญแจทองในการแก้โจทย์เซต!
สำหรับ 3 เซต:
n(A ∪ B ∪ C) = n(A) + n(B) + n(C) – n(A ∩ B) – n(A ∩ C) – n(B ∩ C) + n(A ∩ B ∩ C)
✨ตัวอย่างโจทย์ที่เจอบ่อย
โจทย์: ในห้องเรียนมีนักเรียน 50 คน เรียนคณิตศาสตร์ 30 คน เรียนฟิสิกส์ 25 คน เรียนทั้งสองวิชา 15 คน มีนักเรียนกี่คนที่ไม่เรียนทั้งสองวิชา?
วิธีทำ:
- กำหนด: M = เซตของนักเรียนที่เรียนคณิตศาสตร์, P = เซตของนักเรียนที่เรียนฟิสิกส์
- n(M) = 30, n(P) = 25, n(M ∩ P) = 15
- n(M ∪ P) = 30 + 25 – 15 = 40
- นักเรียนที่ไม่เรียนทั้งสองวิชา = 50 – 40 = 10 คน
✨เทคนิคเด็ดสำหรับสอบ
เครื่องคำนวณโจทย์เซต 👩🏫
วิธีทำ:
แผนภาพเวนน์-ออยเลอร์:
เทคนิคเด็ดสำหรับสอบ 📝
- วาดแผนภาพเสมอ: การวาดแผนภาพเวนน์-ออยเลอร์จะช่วยให้เห็นภาพรวมของโจทย์ได้ชัดเจนขึ้นมาก และลดโอกาสผิดพลาด
- จำสูตรให้แม่น: สูตรพื้นฐานของเซต เช่น $n(A \cup B) = n(A) + n(B) - n(A \cap B)$ เป็นสิ่งที่ต้องจำให้ขึ้นใจ
- ฝึกโจทย์แบบต่างๆ: โจทย์ปัญหาเรื่องเซตมีความหลากหลาย ลองฝึกทำโจทย์หลายๆ รูปแบบจะช่วยให้คุ้นเคยและแก้ปัญหาได้เร็วขึ้น
- ตรวจคำตอบ: หลังจากคำนวณเสร็จ ลองนำตัวเลขที่ได้ไปใส่ในแผนภาพเวนน์-ออยเลอร์ เพื่อตรวจสอบว่าแต่ละส่วนของเซตมีความสมเหตุสมผลและรวมกันได้เท่ากับจำนวนทั้งหมดหรือไม่
- วาดแผนภาพเสมอ – จะช่วยให้เห็นภาพชัดขึ้น
- จำสูตรให้แม่น – สูตรพื้นฐานต้องไม่ผิด
- ฝึกโจทย์แบบต่างๆ – โจทย์เซตมีหลายรูปแบบ
- ตรวจคำตอบ – ใช้แผนภาพตรวจสอบความถูกต้อง
✨สรุป: เซตคือกุญแจสู่ความสำเร็จ
เซต ม.4 ไม่ใช่เรื่องยาก ถ้าเราเข้าใจหลักการและฝึกฝนอย่างต่อเนื่อง การเรียนรู้เรื่องเซตให้แม่นยำจะเป็นรากฐานที่แข็งแกร่งสำหรับการเรียนคณิตศาสตร์ในระดับที่สูงขึ้น
จำไว้ว่า การฝึกฝนคือสิ่งสำคัญที่สุด เริ่มต้นจากโจทย์ง่ายๆ แล้วค่อยๆ เพิ่มความยาก พร้อมกับการวาดแผนภาพประกอบ จะทำให้เข้าใจเรื่องเซตได้อย่างลึกซึ้งและนำไปใช้ในการสอบได้อย่างมั่นใจ!
พร้อมพิชิตเซต ม.4 แล้วหรือยัง? เริ่มต้นจากความเข้าใจพื้นฐาน แล้วไปสู่การเป็นเซียนเซตกันเถอะ!
บทความอื่นๆ เพิ่มเติม 👉 : OnDemand
คอร์สเรียนแนะนำ
โดยพี่ออนดีมานด์