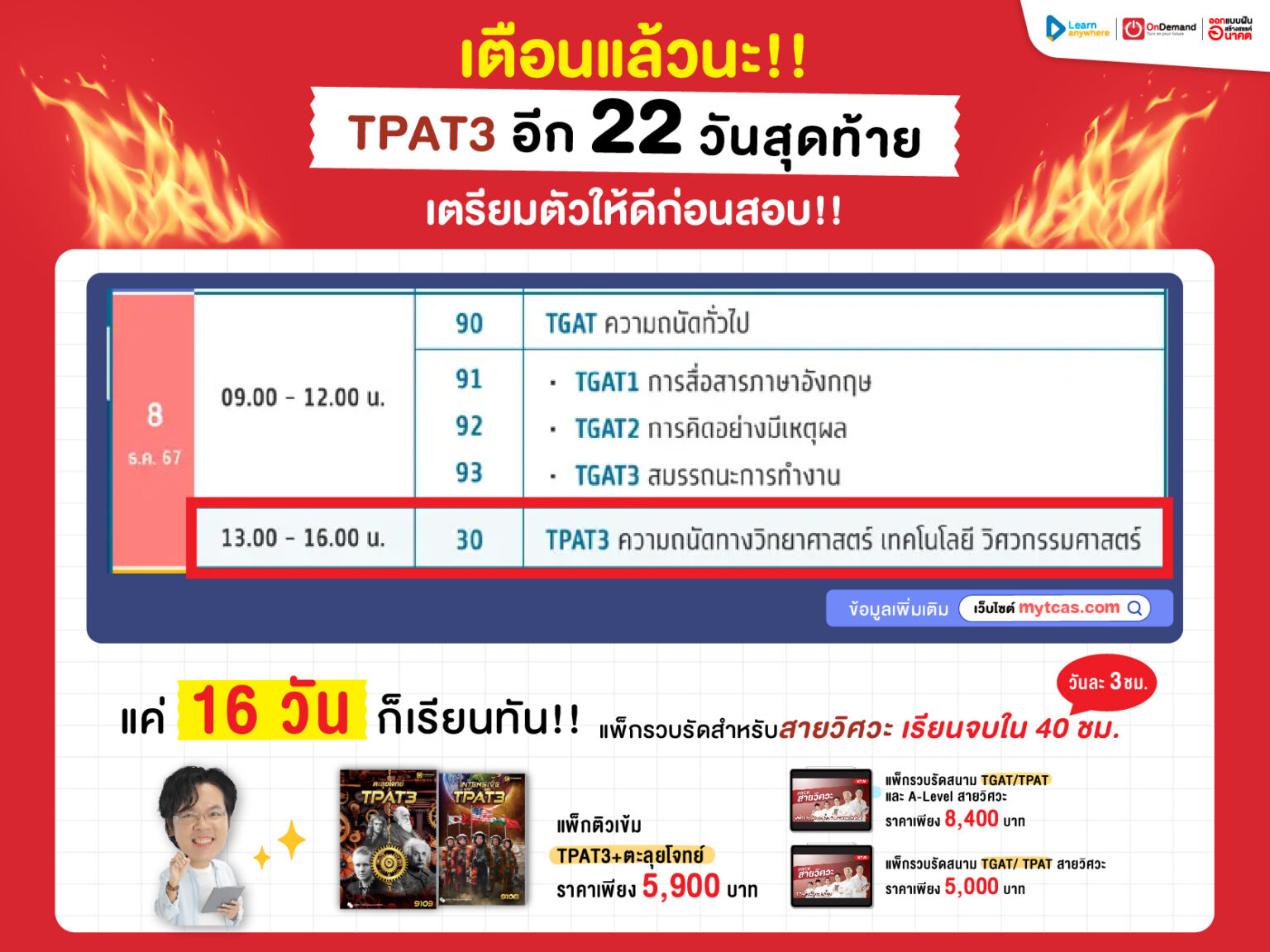
ตรรกศาสตร์ เป็นหนึ่งเนื้อหาหนึ่งในวิชา คณิตศาสตร์ ที่เน้นเกี่ยวกับการหาค่าความจริงของข้อความต่าง ๆ ซึ่งเราจะต้องใช้การคิดแบบเป็นเหตุเป็นผล และเป็นขั้นตอนเพื่อที่จะหาค่าความจริงของข้อความเหล่านั้น โดยวันนี้พี่ก็ได้สรุปเนื้อหาเรื่อง ตรรกศาสตร์ พร้อมตัวอย่างโจทย์มาให้น้อง ๆ แล้วครับ ถ้าพร้อมแล้วไปดูเนื้อหากันเลยย
✨ประพจน์คืออะไร
ประพจน์ คือ ประโยคบอกเล่าหรือประโยคปฏิเสธที่เราสามารถบอกได้ว่าเป็นจริงหรือเท็จอย่างใดอย่างหนึ่งเท่านั้น
เช่น เดือนมกราคมมี 30 วัน
1 เป็นจำนวนคี่
สงขลาเป็นจังหวัดในภาคเหนือของไทย
เป็นต้น
ประโยคที่ไม่เป็นประพจน์ คือ ประโยคที่ไม่สามารถบอกได้ว่าเป็นจริงหรือเท็จอย่างใดอย่างหนึ่ง (ประโยค คำถาม คำสั่ง ขอร้อง อุทาน)
เช่น ห้ามส่งเสียงดัง
เธอไปไหนมา
x + 2 = 10
เป็นต้น
การหาค่าความจริงของประพจน์
ตัวเชื่อมประพจน์
สำหรับตัวเชื่อมประพจน์ทางตรรกศาสตร์นั้นจะมีอยู่ 5 ตัวดังนี้ครับ

และเรามักจะใช้ตัวอักษรภาษาอังกฤษตัวพิมพ์เล็กเพื่อแทนประพจน์ต่าง ๆ เช่น p, q, r, s, \dots เช่น
p และ q จะเขียนแทนด้วย p \land q
p หรือ q จะเขียนแทนด้วย p \lor q
ถ้า p แล้ว q จะเขียนแทนด้วย p \longrightarrow q
p ก็ต่อเมื่อ q จะเขียนแทนด้วย p \longleftrightarrow q
นิเสธของ p จะเขียนแทนด้วย \sim p
ตารางค่าความจริง
กำหนดให้ p, q เป็นประพจน์ ถ้าเรานำ p, q มาเชื่อมกันด้วยตัวเชื่อมทั้ง 5 ตัว เราจะได้ตารางค่าความจริงดังนี้ครับ
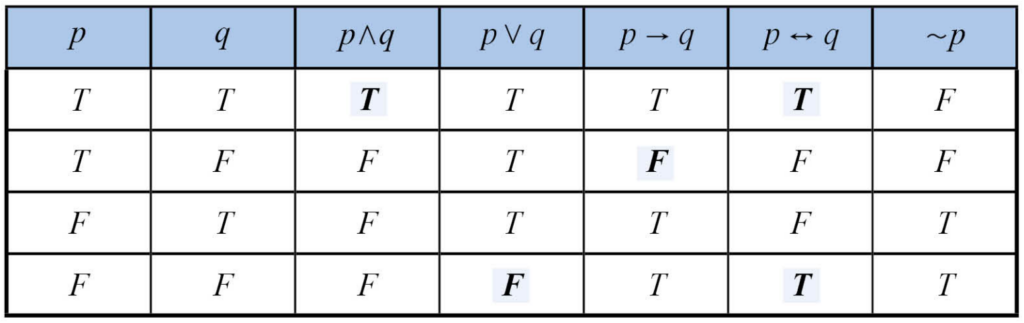
โดยที่ T, F หมายถึงจริงและเท็จตามลำดับ
จากตารางค่าความจริงข้างต้น เราจะพบว่ามีสิ่งที่น่าสนใจดังนี้ครับ

ลำดับในการหาค่าความจริง
เมื่อเรามีตัวเชื่อมหลายตัว เราต้องยึดลำดับในการหาค่าความจริงตามลำดับต่อไปนี้ครับ
- วงเล็บ
- \sim
- \land \, \, \lor
- \longrightarrow
- \longleftrightarrow
สำหรับตัวเชื่อม \land \, \, \lor นั้นมีความสำคัญเท่ากัน ให้น้อง ๆ หาค่าความจริงตามลำดับจากซ้ายไปขวาครับ
เมื่อเราทราบแบบนี้แล้ว ต่อไปเราจะลองมาหาค่าความจริงกันดูนะครับ
ตัวอย่างที่ 1 กำหนดให้ p, q, r เป็นประพจน์ที่มีค่าความจริงเป็น จริง เท็จ จริง ตามลำดับ จงหาค่าความจริงของ p \longrightarrow (q \lor \sim r)
วิธีทำ
\begin{aligned}p \longrightarrow (q \lor \sim r)&\equiv T \longrightarrow (F \lor \sim T) \\&\equiv T \longrightarrow (F \lor F) \\&\equiv T \longrightarrow F \\&\equiv F \\\end{aligned}
ดังนั้นจึงสรุปได้ว่า p \longrightarrow (q \lor \sim r) มีค่าความจริงเป็นเท็จ
✨สมมูล
ความหมายของสมมูล
ประพจน์ p สมมูลกับ q ก็ต่อเมื่อ ประพจน์ p กับประพจน์ q มีค่าความจริงเหมือนกันกรณีต่อกรณี และเราจะใช้สัญลักษณ์เป็นขีดสามขีดคล้าย ๆ เครื่องหมายนเท่ากับ ที่พี่ได้ใช้ไปในตัวอย่างก่อนหน้านี้ นั่นคือ \equiv นั่นเองครับ โดยถ้าเราจะบอกว่า p สมมูลกับ q เราจะสามารถเขียนได้ว่า p \equiv q นั่นเองครับ
ตัวอย่างที่ 2 จงพิจารณาว่า p \longrightarrow q สมมูลกับ \sim p \lor q หรือไม่
วิธีทำ
เราจะสร้างตารางค่าความจริงได้ดังนี้ครับ
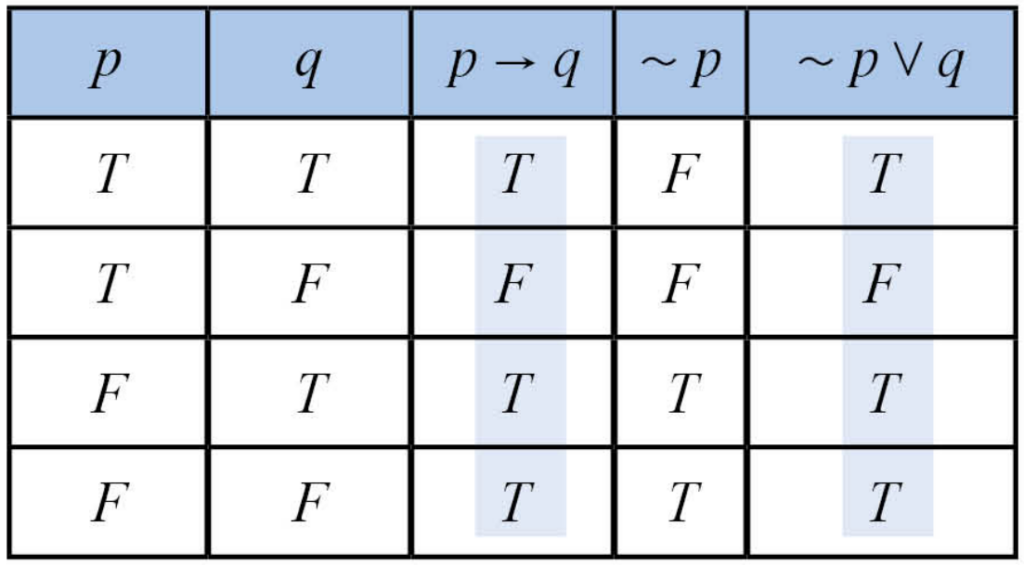
เราจะพบว่าค่าความจริงของทั้งสองนั้นมันเหมือนกันแบบกรณีต่อกรณีเลย เราจะสามารถสรุปได้เลยครับว่า p \longrightarrow q \equiv \sim p \lor q นั่นเอง
โดยประพจน์ที่สมมูลกันที่สำคัญ ๆ จะมีทั้งหมด 7 กลุ่มตามตารางต่อไปนี้ที่พี่ได้สรุปมาให้น้อง ๆ ครับ
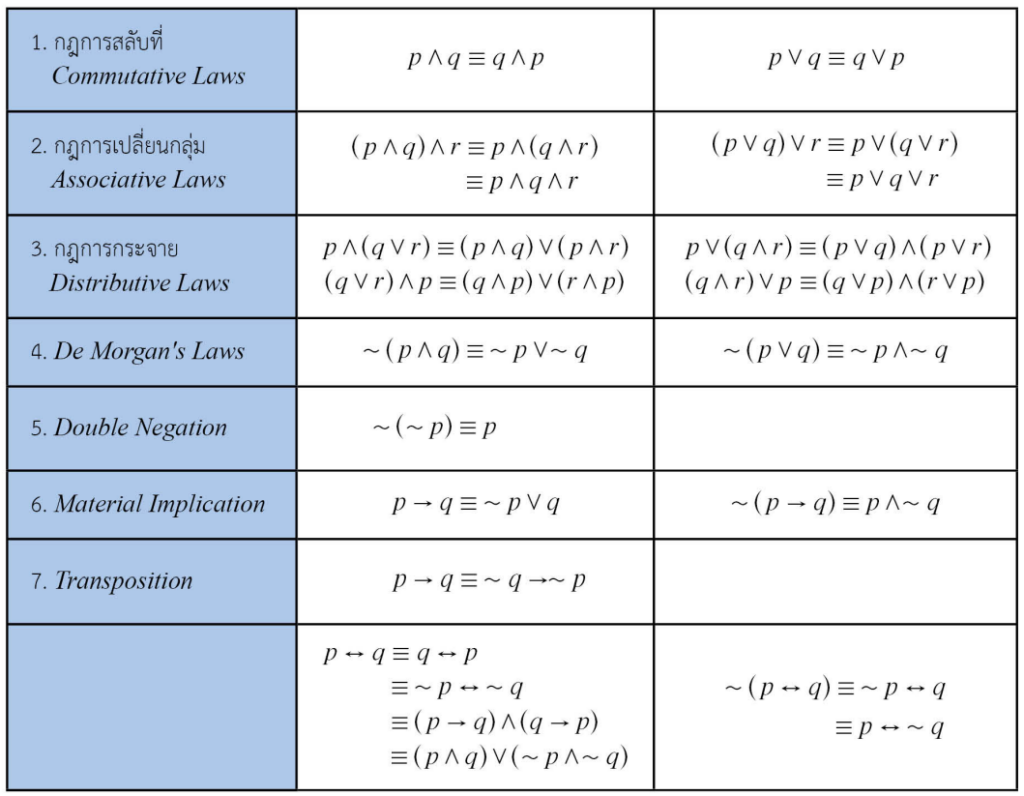
น้อง ๆ สามารถหยิบไปใช้ได้ทันทีเลยว่าประพจน์ไหนสมมูลกับประพจน์ไหน จะทำให้เราแก้โจทย์บางข้อได้ง่ายขึ้นครับ
✨สัจนิรันดร์
ความหมายของสัจนิรันดร์
ประพจน์ที่เป็นสัจนิรันดร์ คือ ประพจน์ที่มีค่าความจริงเป็นจริงทุกกรณี
การพิสูจน์สัจนิรันดร์
ในการพิสูจน์หรือตรวจสอบว่าประพจน์ใด ๆ เป็นสัจนิรันดร์หรือไม่นั้น พี่ขอนำเสนอ 2 วิธีดังนี้ครับ
- การสร้างตารางค่าความจริง
เพื่อกระจายออกมาดูชัด ๆ เลยว่า เป็นจริงทุกกรณีมั้ย หรือมีกรณีที่ไม่เป็นจริงครับ
ตัวอย่างที่ 3 จงพิจารณาว่า (p \longrightarrow q) \longrightarrow (\sim p \lor q) เป็นสัจนิรันดร์หรือไม่
วิธีทำ
เราจะสร้างตารางค่าความจริงได้ดังนี้ครับ
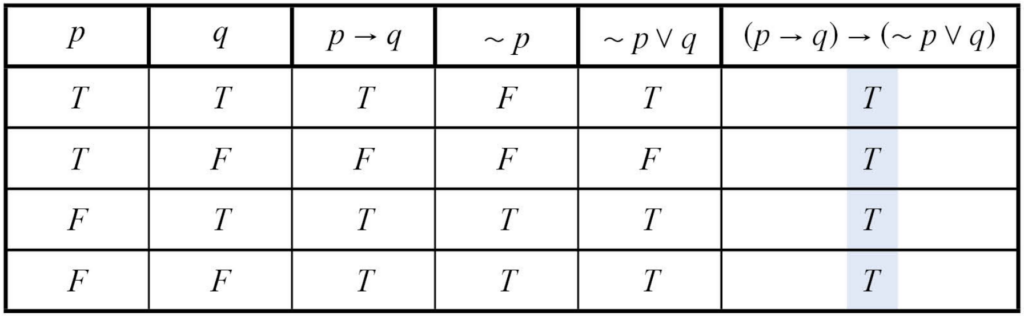
เราจะพบว่าค่าความจริงของ (p \longrightarrow q) \longrightarrow (\sim p \lor q) นั้น เป็นจริงทุกกรณีเลย ไม่ว่า p, q จะมีค่าความจริงเป็นแบบไหนก็ตาม ดังนั้นเราจึงสามารถสรุปได้เลยครับว่า (p \longrightarrow q) \longrightarrow (\sim p \lor q) เป็นสัจนิรันดร์
- การหาข้อขัดแย้ง
หลักการคือการที่เราสมมุติไปก่อนเลยว่าประพจน์ที่จะตรวจสอบนั้นเป็นเท็จ (แต่จริง ๆ อาจจะไม่ใช่ก็ได้) แล้วไล่ดูว่า ถ้าเป็นเท็จแล้ว ประพจน์แต่ละประพจน์จะต้องเป็นจริงหรือเท็จ หากระหว่างนั้น พบว่ามีประพจน์บางตัวเป็นได้ทั้งจริงและเท็จ แสดงว่าเกิดข้อขัดแย้ง ดังนั้นการที่เราสมมุติว่าทั้งประพจน์นี้เป็นเท็จนั้นจึงไม่จริง เลยจะต้องสรุปว่าเป็นจริงแทน นั่นคือ เป็นสัจนิรันดร์นั่นเองครับ
โดยพี่ได้สรุปเป็นขั้นตอนตามแผนภาพนี้ครับ

ตัวอย่างที่ 4 จงพิจารณาว่า (p \longrightarrow q) \longrightarrow (\sim p \lor q) เป็นสัจนิรันดร์หรือไม่ โดยใช้วิธีการหาข้อขัดแย้ง
วิธีทำ
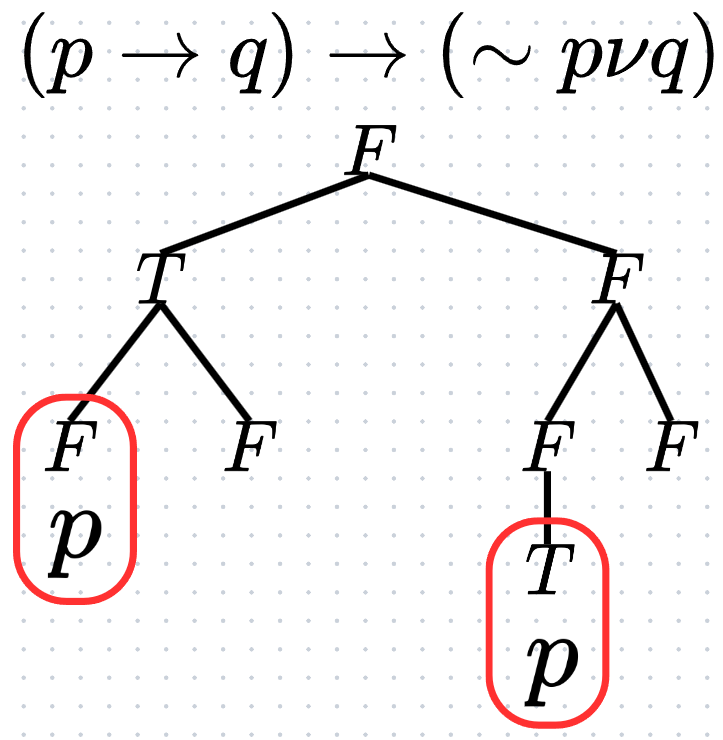
โดยวิธีการหาข้อขัดแย้ง เราจะพบว่าในกรอบสีแดงทั้งสอง p มีค่าความจริงเป็นเท็จ และ จริง พร้อม ๆ กัน เมื่อเป็นเช่นนี้ เราจึงสรุปว่าเกิดข้อขัดแย้ง และทำให้ (p \longrightarrow q) \longrightarrow (\sim p \lor q) เป็นสัจนิรันดร์นั่นเองครับ
✨การอ้างเหตุผล
หลักการของการอ้างเหตุผลนั้นเราจะสนใจว่าการอ้างเหตุและผลนั้นสมเหตุสมผลกันหรือไม่
- ถ้าทำตามเหตุ แล้วได้ผลอย่างที่อ้าง ก็แสดงว่า การอ้างเหตุผลนั้นสมเหตุสมผล
- แต่ ถ้าทำตามเหตุ แล้วไม่ได้ผลอย่างที่อ้าง ก็แสดงว่า การอ้างเหตุผลนั้นไม่สมเหตุสมผล
- ส่วน ถ้าไม่ทำตามเหตุ แล้วได้ผลตามที่อ้างหรือไม่ได้ ก็ไม่สามารถบอกได้ว่าสิ่งที่พูดมานั้นสมเหตุสมผลหรือไม่
หรือสรุปง่าย ๆ ก็คือ ถ้า p_1, p_2, p_3, \dots, p_n เป็นเหตุ และ C เป็นผล ให้เรานำ p_1, p_2, p_3, \dots, p_n มาเชื่อมกันด้วยตัวเชื่อม “และ” แล้วเชื่อมเหตุทั้งหมดกับผลด้วยตัวเชื่อม “ถ้าแล้ว” แล้วตรวจสอบต่อ ถ้าเป็นสัจนิรันดร์ก็สรุปได้เลยว่าสมเหตุสมผล แต่ถ้าไม่เป็นสัจนิรันดร์ ก็ไม่สมเหตุสมผลนั่นเองครับ
ตัวอย่างที่ 5 จงพิจารณาว่าการอ้างเหตุผลต่อไปนี้สมเหตุสมผลหรือไม่
เหตุ
- p \longrightarrow (q \lor r)
- \sim q \land p
ผล r
วิธีทำ
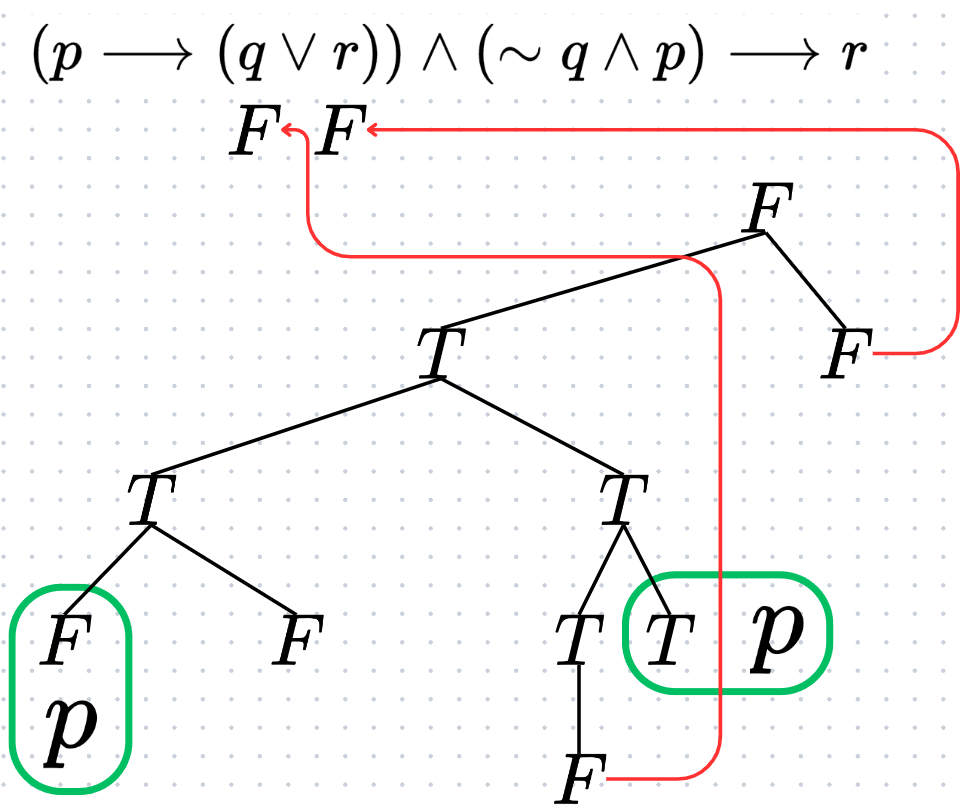
เราจะพบว่าในกรอบสีเขียวทั้งสอง p มีค่าความจริงเป็นเท็จ และ จริง พร้อม ๆ กัน เมื่อเป็นเช่นนี้ เราจึงสรุปว่าเกิดข้อขัดแย้ง ทำให้ประพจน์ดังกล่าวเป็นสัจนิรันดร์ จึงทำให้การอ้างเหตุผลนี้สมเหตุสมผลนั่นเองครับ
✨ประโยคเปิดและตัวบ่งปริมาณ
ความหมายของประโยคเปิด
ประโยคเปิด คือ ประโยคบอกเล่าหรือปฏิเสธที่มีตัวแปร และเมื่อเราแทนค่าตัวแปรในประโยคเปิด จะทำให้ประโยคเปิดกลายเป็นประพจน์ เพราะเราสามารถบอกค่าความจริงได้นั่นเอง
เช่น 3x + 1 = 7, y+x = 5, เขาเป็นนักเรียน เหล่านี้ถือว่าเป็นประโยคเปิด
เราจะใช้ P(x), P(x, y) แทนประโยคเปิดที่มีตัวแปร 1, 2 ตัวตามลำดับ
ตัวบ่งปริมาณ
ตัวบ่งปริมาณจะมีอยู่ 2 แบบ ดังนี้ครับ
- for all x (\forall x) หมายถึง
สำหรับทุก x, สำหรับ x ทุกตัว, แต่ละ x
- for some x (\exists x) หมายถึง
มี x อย่างน้อย 1 ตัว, มี x บางตัว, สำหรับ x บางตัว
ซึ่งเราสามารถทำประโยคเปิดให้กลายเป็นประพจน์โดยการเติมตัวบ่งปริมาณและเอกภพสัมพัทธ์เข้าไป เพราะถ้าทำแบบนั้นแล้ว เราจะสามารถบอกค่าความจริงของมันได้นั่นเองครับ
เช่น สำหรับจำนวนจริง x ทุกจำนวน x^2 \geq 0
มีจำนวนเต็ม x บางจำนวนที่ทำให้ x+1 < 5 เป็นตัน
โจทย์ส่วนใหญ่ ถ้าไม่ได้กำหนดเอกภพสัมพัทธ์มาให้ ให้น้อง ๆ ถือว่าเอกภพสัมพัทธ์สำหรับข้อนั้น ๆ คือเซตของจำนวนจริงครับ
ค่าความจริงของประโยคเปิดที่มีตัวบ่งปริมาณ
สำหรับค่าความจริงของประโยคเปิดที่มีตัวบ่งปริมาณน้อง ๆ สามารถยึดหลักนี้ได้เลยย

เป็นยังไงกันบ้างครับ กับเนื้อหา ตรรกศาสตร์ เบื้องต้นและการให้เหตุผลที่พี่นำมาฝากน้อง ๆ ในวันนี้ หลายคนอาจจะยังไม่เข้าใจในครั้งแรกที่อ่าน แต่น้อง ๆ ไม่ต้องกังวล เพราะเราไม่จำเป็นต้องเข้าใจเนื้อหาทั้งหมดนี้ภายในวันเดียวหรือการอ่านเพียงรอบเดียวก็ได้ครับ เราสามารถค่อย ๆ ทบทวนเนื้อหาไปพร้อมกับการฝึกทำโจทย์เพื่อให้เก่งขึ้นได้ครับบ
บทความอื่นๆ เพิ่มเติม 👉 : OnDemand
คอร์สเรียนแนะนำ
โดยพี่ออนดีมานด์